某厂使用两种零件A、B装配两种产品P、Q，该厂的生产能力是月产P产品最多有2500件，月产Q产品最多有1200件；而且组装一件P产品要4个A、2个B，组装一件Q产品要6个A、8个B，该厂-数学

题目简介

题目详情

某厂使用两种零件A、B装配两种产品P、Q，该厂的生产能力是月产P产品最多有2500件，月产Q产品最多有1200件；而且组装一件P产品要4个A、2个B，组装一件Q产品要6个A、8个B，该厂在某个月能用的A零件最多14000个；B零件最多12000个．已知P产品每件利润1000元，Q产品每件2000元，欲使月利润最大，需要组装P、Q产品各多少件？最大利润多少万元？

题型：解答题难度：中档来源：不详

答案

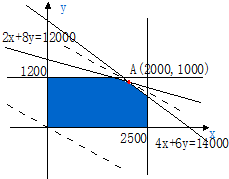
设分别生产P、Q产品x件、y件，则有

4x+6y≤14000

2x+8y≤12000

0≤x≤2500

0≤y≤1200

…（3分）
设利润 z=1000x+2000y=1000（x+2y） …（4分）
要使利润最大，只需求z的最大值．
作出可行域如图示（阴影部分及边界）…（6分）
作出直线l：1000（x+2y）=0，即x+2y=0
由于向上平移平移直线l时，z的值增大，所以在点A处z取得最大值…（8分）
由

2x+3y=7000

x+4y=6000

解得

x=2000

y=1000

，即A（2000，1000）…（10分）
因此，此时最大利润zmax=1000（x+2y）=4000000=400（万元）．…（11分）
答：要使月利润最大，需要组装P、Q产品2000件、1000件，此时最大利润为400万元．…（12分）

上一篇 : 某公司生产甲、乙两种桶装产品
下一篇 : 若实数x、y满足条件x≤3x+y≥0

某厂使用两种零件A、B装配两种产品P、Q，该厂的生产能力是月产P产品最多有2500件，月产Q产品最多有1200件；而且组装一件P产品要4个A、2个B，组装一件Q产品要6个A、8个B，该厂-数学

题目简介

题目详情

答案

更多内容推荐