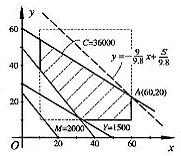
 (1)变量情况. 主要变量:限制在10秒和60秒之间的两次广告时间; 制约变量:总的费用≤36000元,需影响年轻人数≥1500千人, 需影响中年人数≥2000千人,需影响老年人数≥2000千人. (2)变量间的关系: 总的费用=(购买的时间×每秒价格)之和; 影响的人数=(购买的时间×相应年龄组每秒影响的人数)之和; 销售额=(占影响人数的份额×对应组影响的人数)之和. (3)建模与求记x、y分别表示早、晚购买的时间(秒); S=第一个月的销售额(用千人表示),C=总的费用(元); Y、M、O分别表示年轻、中年、老年组受到广告影响的人数(千人). 于是有: C=400x+600y≤3600, Y=30x+50y≥1500, M=100x+80y≥2000,(*) O=50x+40y≥2000, 10≤x≤60,10≤y≤60 要求S=0.1Y+0.05M+0.02O=9x+9.8y的最大值. 符合约束条件(*)的点(x,y)在如上图所示的六边形区域内, 求S=9x+9.8y的最大值转化为求直线y=9x/9.8+S/9.8的截距S/9.8的最大值. 由图知,当此直线过图中直线400x+600y=3600和x=60的交点A(60,20)时, 截距最大,此时Smax=9×60+9.8×20=736(千人). (4)结论:如上讨论可知,满意的结果是第一个月的销售额是736000(份) 只要购买晚八叫点前60秒和九点后20秒的广告即可. 此时,花掉了所有的预算并超过所有年龄组所要求影响的人数. |
题目简介
某公司准备推出一个新产品,打算拨出款项3万6千元在本地的电视台做广告,.当地电视台广告部安排该公司的广告在晚上八点前和九点后做广告.晚八点前的广告每秒400元,九点后的-数学
题目详情
根据市场调查研究表明,受广告影响的人数依赖于广告播出的时间以及年龄层次,受广告影响的人数总是和广告播出的时间成正比例.广告时每秒影响各年龄组的人数(千人)估计如表所示.
现在的要求是广告宣传至少要影响1500000个年轻人,2000000个中年人和2000000个老年人.该公司也估计了在第一个月内受广告影响的人中,每10个年轻人中有1人、20个中年人中1人、50个老年人中1人将购买一件新产品<并且假设没有一个人第二次再买>,则若使第一个月的销售额最大,如何来安排广告?