 设购买桌子x张,椅子y张,其总数为z, 根据题意得约束条件为
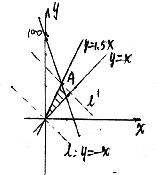
目标函数为z=x+y,作出可行域 作出直线l:x+y=0将l向右上方平称到l′位置,使l′经过直线y=1.5x与50x+20y≤2000 的交点A,此时z应取得最大值. 解
又由50x+20y≤2000.得y=37. ∴x=25,y=37是符合条件的最优解 答:应买桌子25张,椅子37张. |
 设购买桌子x张,椅子y张,其总数为z, 根据题意得约束条件为
目标函数为z=x+y,作出可行域 作出直线l:x+y=0将l向右上方平称到l′位置,使l′经过直线y=1.5x与50x+20y≤2000 的交点A,此时z应取得最大值. 解
又由50x+20y≤2000.得y=37. ∴x=25,y=37是符合条件的最优解 答:应买桌子25张,椅子37张. |
题目简介
预算用2000元购买单价为50元的桌子和20元的椅子,希望使桌椅的总数尽可能的多,但椅子数不少于桌子数且不多于桌子数的1.5倍,问桌、椅各买多少才行?-数学
题目详情