| 证明:如图,延长AP交⊙O2于点Q, 连接AH,BD,QB,QC,QH. 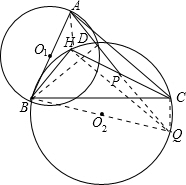 因为AB为⊙O1的直径, 所以∠ADB=∠BDQ=90°.(5分) 故BQ为⊙O2的直径. 于是CQ⊥BC,BH⊥HQ.(10分) 又因为点H为△ABC的垂心,所以AH⊥BC,BH⊥AC. 所以AH∥CQ,AC∥HQ, 四边形ACQH为平行四边形.(15分) 所以点P为CH的中点.(20分) |
| 证明:如图,延长AP交⊙O2于点Q, 连接AH,BD,QB,QC,QH.  因为AB为⊙O1的直径, 所以∠ADB=∠BDQ=90°.(5分) 故BQ为⊙O2的直径. 于是CQ⊥BC,BH⊥HQ.(10分) 又因为点H为△ABC的垂心,所以AH⊥BC,BH⊥AC. 所以AH∥CQ,AC∥HQ, 四边形ACQH为平行四边形.(15分) 所以点P为CH的中点.(20分) |
题目简介
如图,点H为△ABC的垂心,以AB为直径的⊙O1和△BCH的外接圆⊙O2相交于点D,延长AD交CH于点P,求证:点P为CH的中点.-数学
题目详情
CH于点P,
求证:点P为CH的中点.