 (1)证明:过点A作AF⊥BC于F, ∵AB=AC, ∴FC=
∵AD∥BC, ∴四边形ADCF是平行四边形, ∵∠AFC=90°, ∴四边形ADCF是矩形, ∴∠ADC=90°; (2)∵∠ADC=90°,AC=6,AD=2, ∴CD=4
∴sin∠ABC=
∵AD∥BC, ∴△AED∽△CEB, ∴
∵BD=
∴BE=
|
 (1)证明:过点A作AF⊥BC于F, ∵AB=AC, ∴FC=
∵AD∥BC, ∴四边形ADCF是平行四边形, ∵∠AFC=90°, ∴四边形ADCF是矩形, ∴∠ADC=90°; (2)∵∠ADC=90°,AC=6,AD=2, ∴CD=4
∴sin∠ABC=
∵AD∥BC, ∴△AED∽△CEB, ∴
∵BD=
∴BE=
|
题目简介
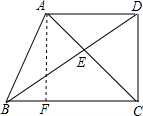
如图,梯形ABCD中,AD∥BC,AB=AC,BC=2AD,对角线AC、BD相交于点E.(1)求证:∠ADC=90°;(2)若AC=6,AD=2,求∠ABC的正弦值和线段BE长.-数学
题目详情
(1)求证:∠ADC=90°;
(2)若AC=6,AD=2,求∠ABC的正弦值和线段BE长.