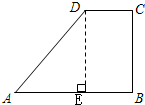
 (1)过点D作DE⊥AB,垂足为点E, 设AE=x,则AD=x+1.(11分) 根据题意,在Rt△ADE中,AD2=AE2+DE2. ∴x2+9=(x+1)2,(1分) 解得x=4.(1分) 即AE=4,AD=5, ∴cos∠A=
(2)∵AB∥CD, ∴∠BDC=∠ABD 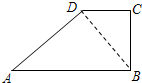 , ∵∠ABC=90°,△ADB∽△BCD, ∴△ADB是直角三角形,且∠ADB=90°.(1分) ∴∠DBC=∠A, 在△BCD中,由CD=1,cot∠DBC=cotA=x得,BC=x,(1分) 从而DB=
由△ABD∽△BDC得,
即
∴y=x2+1. |
题目简介
如图,已知梯形ABCD中,AB∥CD,∠ABC=90°,CD=1.(1)若BC=3,AD=AB,求∠A的余弦值;(2)连接BD,若△ADB与△BCD相似,设cotA=x,AB=y,求y关于x的函数关系
题目详情
(1)若BC=3,AD=AB,求∠A的余弦值;
(2)连接BD,若△ADB与△BCD相似,设cotA=x,AB=y,求y关于x的函数关系式.