(Ⅰ)取AD的中点N,连接MN,NF.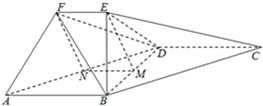 在△DAB中,M是BD的中点,N是AD的中点, ∴MN∥AB,MN=
又∵EF∥AB,EF=
∴四边形MNFE为平行四边形,可得EM∥FN. 又∵FN?平面ADF,EM?平面ADF, ∴EM∥平面ADF.…(6分) (Ⅱ)假设在EB上存在一点P,使得∠CPD最大. ∵EB⊥平面ABD,CD?平面ABD,∴EB⊥CD. 又∵CD⊥BD,EB∩BD=B,∴CD⊥平面EBD.…(8分) 在Rt△CPD中,tan∠CPD=
∵CD为定值,且∠CPD为锐角, ∴要使∠CPD最大,只要DP最小即可.显然,当DP⊥EB时,DP最小. 因此DB⊥EB,所以当点P在点B处时,使得∠CPD最大.…(11分) Rt△PCD中,tan∠CPD=
所以在EB上存在一点P,使得∠CPD最大,且∠CPD的正切值为
|
题目简介
在如图所示的几何体中,四边形ABCD为平行四边形,∠ABD=90°,EB⊥平面ABCD,EF∥AB,AB=2,EF=1,BC=13,且M是BD的中点.(Ⅰ)求证:EM∥平面ADF;(Ⅱ)在EB上是否存
题目详情
(Ⅰ)求证:EM∥平面ADF;
(Ⅱ)在EB上是否存在一点P,使得∠CPD最大?若存在,请求出∠CPD的正切值;若不存在,请说明理由.