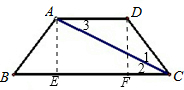
 过点A作AE⊥BC,垂足为E,过点D作DF⊥BC,垂足为F,如下图所示, ∵AC平分∠BCD, ∴∠1=∠2. ∵AD∥BC, ∴∠2=∠3. ∴∠1=∠3. ∴AD=DC.∵AD=5,AB=DC, ∴AD=DC=AB=5. 过点A作AE⊥BC于点E,过点D作DF⊥BC于点F. ∴∠AEB=90°. 在Rt△AEB中, tanB=
设AE=3x,则BE=4x. ∵AB=5, ∴(3x)2+(4x)2=52. ∴x=1(负值舍去). ∴AE=3,BE=4.同理可得FC=4. ∵AE⊥BC,DF⊥BC, ∴AE∥DF. ∵AD∥BC, ∴四边形AEFD是平行四边形. ∴EF=AD=5. ∴BC=13. |
题目简介
已知:如图,AD∥BC,AB=CD,对角线CA平分∠BCD,AD=5,tanB=34,求BC的长.-数学
题目详情