 连接OC. ∵气球的直径为4m,∴半径为2m,∵测得气球的视角∠BAC=2°(AB、AC为⊙O的切线,B、C为切点), ∴∠OAC=1°, 在Rt△OAC中,OC=2m,∠OAC=1°, ∵sin1°=
∴AO=
在Rt△OAD中,有OD=OA×sin60°≈99(m). 答:气球中心O离地面的高度OD约为99m. |
 连接OC. ∵气球的直径为4m,∴半径为2m,∵测得气球的视角∠BAC=2°(AB、AC为⊙O的切线,B、C为切点), ∴∠OAC=1°, 在Rt△OAC中,OC=2m,∠OAC=1°, ∵sin1°=
∴AO=
在Rt△OAD中,有OD=OA×sin60°≈99(m). 答:气球中心O离地面的高度OD约为99m. |
题目简介
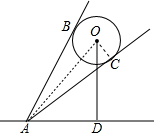
如图,挂着“庆祝海门实验学校建校三周年”条幅的氢气球升在校园上空,已知气球的直径为4m,在地面A点测得气球中心O的仰角为∠OAD=60°,测得气球的视角∠BAC=2°(AB、AC为⊙O的切线-数学
题目详情
(精确到1m,参考数据:sin1°=0.0175,sin2°=0.0349,tan1°=0.0175,tan2°=0.0350,