 (1)证明:过C点作CH∥BD,交AB的延长线于点H; 连接AC,交EF于点K,则AK=CK. ∵AB∥CD,∴BH=CD,BD=CH. ∵AD=BC,∴AC=BD=CH. ∵CE⊥AB, ∴AE=EH. ∴EK是△AHC的中位线. ∴EK∥CH. ∴EF∥BD. (2)由(1)得BH=CD,EF∥BD. ∴∠AEF=∠ABD. ∵AB=7,CD=3, ∴AH=10. ∵AE=CE,AE=EH, ∴AE=CE=EH=5. ∵CE⊥AB,∴CH=5
∵∠EAF=∠BAD,∠AEF=∠ABD, ∴△AFE∽△ADB. ∴
∴EF=
|
题目简介
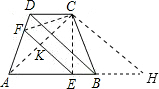
如图,四边形ABCD为一梯形纸片,AB∥CD,AD=BC.翻折纸片ABCD,使点A与点C重合,折痕为EF.已知CE⊥AB.(1)求证:EF∥BD;(2)若AB=7,CD=3,求线段EF的长.-数学
题目详情
(1)求证:EF∥BD;
(2)若AB=7,CD=3,求线段EF的长.