 (1)∵CD⊥平面ABC,BE⊥平面ABC∴CD∥BE,∴CD∥平面ABE 又l=平面ACD∩平面ABE ∴CD∥l 又l?平面BCDE,CD?平面BCDE ∴l∥平面BCDE. (2)存在,F是BC的中点, 下加以证明: ∵CD⊥平面ABC ∴CD⊥AF ∵AB=AC,F是BC的中点 ∴AF⊥BC,AF⊥平面BCDE ∴AF⊥DF,AF⊥EF ∴∠DFE是面AFD和面AFE所成二面角的平面角 在△DEF中,FD=
FD⊥FE,即∠DFE=90° ∴平面AFD⊥平面AFE |
 (1)∵CD⊥平面ABC,BE⊥平面ABC∴CD∥BE,∴CD∥平面ABE 又l=平面ACD∩平面ABE ∴CD∥l 又l?平面BCDE,CD?平面BCDE ∴l∥平面BCDE. (2)存在,F是BC的中点, 下加以证明: ∵CD⊥平面ABC ∴CD⊥AF ∵AB=AC,F是BC的中点 ∴AF⊥BC,AF⊥平面BCDE ∴AF⊥DF,AF⊥EF ∴∠DFE是面AFD和面AFE所成二面角的平面角 在△DEF中,FD=
FD⊥FE,即∠DFE=90° ∴平面AFD⊥平面AFE |
题目简介
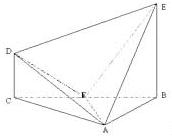
在几何体ABCDE中,∠BAC=π2,DC⊥平面ABC,EB⊥平面ABC,AB=AC=BE=2,CD=1.(1)设平面ABE与平面ACD的交线为直线l,求证:l∥平面BCDE;(2)在棱BC上是否存在
题目详情
(1)设平面ABE与平面ACD的交线为直线l,求证:l∥平面BCDE;
(2)在棱BC上是否存在一点F使得平面AFD⊥平面AFE.