| (1)证明:∵BC=AC,E为AB的中点, ∴AB⊥CE. 又∵AD=BD,E为AB的中点 ∴AB⊥DE. ∵DE∩CE=E ∴AB⊥平面DCE; (2)证明:由(1)有AB⊥平面DCE, 又∵AB?平面ABC, ∴平面CDE⊥平面ABC. (3)在AB上取一点F,使AF=2FE,则可得GF∥平面CDE 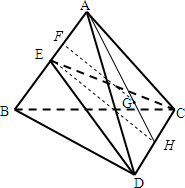 取DC的中点H,连AH、EH ∵G为△ADC的重心, ∴G在AH上,且AG=2GH,连FG,则FG∥EH 又∵FG?平面CDE,EH?平面CDE, ∴GF∥平面CDE. |
| (1)证明:∵BC=AC,E为AB的中点, ∴AB⊥CE. 又∵AD=BD,E为AB的中点 ∴AB⊥DE. ∵DE∩CE=E ∴AB⊥平面DCE; (2)证明:由(1)有AB⊥平面DCE, 又∵AB?平面ABC, ∴平面CDE⊥平面ABC. (3)在AB上取一点F,使AF=2FE,则可得GF∥平面CDE  取DC的中点H,连AH、EH ∵G为△ADC的重心, ∴G在AH上,且AG=2GH,连FG,则FG∥EH 又∵FG?平面CDE,EH?平面CDE, ∴GF∥平面CDE. |
题目简介
如图,已知空间四边形ABCD中,BC=AC,AD=BD,E是AB的中点,求证:(1)AB⊥平面CDE;(2)平面CDE⊥平面ABC;(3)若G为△ADC的重心,试在线段AE上确定一点F,使得GF∥平面
题目详情
(1)AB⊥平面CDE;
(2)平面CDE⊥平面ABC;
(3)若G为△ADC的重心,试在线段AE上确定一点F,使得GF∥平面CDE.