 证明:∵PO⊥平面ABCD,AD∥PO, ∴DA⊥AB,PO⊥AB 又DA=AO=
又AO=
又PB?平面OCD,OD?平面COD.∴PB∥平面COD. (II)依题意可设OA=a,则PO=OB=OC=2a,DA=a, 由DA∥PO,且PO⊥平面ABC, 知DA⊥平面ABC. 从而PD=DO=
在△PDO中∵PD=DO=
又∵OC=OB=2a,∠ABC=45°,∴CO⊥AB 又PO⊥平面ABC,∴CO⊥平面PAB、 故CO⊥PD. ∵CO与DO相交于点O. ∴PD⊥平面COD. |
 证明:∵PO⊥平面ABCD,AD∥PO, ∴DA⊥AB,PO⊥AB 又DA=AO=
又AO=
又PB?平面OCD,OD?平面COD.∴PB∥平面COD. (II)依题意可设OA=a,则PO=OB=OC=2a,DA=a, 由DA∥PO,且PO⊥平面ABC, 知DA⊥平面ABC. 从而PD=DO=
在△PDO中∵PD=DO=
又∵OC=OB=2a,∠ABC=45°,∴CO⊥AB 又PO⊥平面ABC,∴CO⊥平面PAB、 故CO⊥PD. ∵CO与DO相交于点O. ∴PD⊥平面COD. |
题目简介
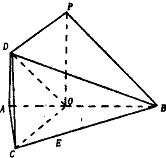
如图,在△ABC中,已知∠ABC=45°,O在AB上,且OB=OC=23AB,又P0⊥平面ABC,DA∥PO,DA=AO=12PO.(I)求证:PB∥平面COD;(II)求证:PD⊥平面COD.-数学
题目详情
(I)求证:PB∥平面COD;
(II)求证:PD⊥平面COD.