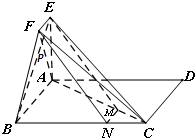
 (Ⅰ)因为EF∥AB,所以EF与AB确定平面EABF, 因为EA⊥平面ABCD,所以EA⊥BC.…(2分) 由已知得AB⊥BC且EA∩AB=A, 所以BC⊥平面EABF.…(3分) 又AF?平面EABF, 所以BC⊥AF.…(4分) (Ⅱ)过M作MN⊥BC,垂足为N,连结FN,则MN∥AB.…(5分) 又CM=
又EF∥AB且EF=
且EF=MN,所以四边形EFNM为平行四边形.…(7分) 所以EM∥FN. 又FN?平面FBC,EM?平面FBC, 所以EM∥平面FBC.…(9分) (Ⅲ)直线AF垂直于平面EBC.…(10分) 证明如下: 由(Ⅰ)可知,AF⊥BC. 在四边形ABFE中,AB=4,AE=2,EF=1,∠BAE=∠AEF=90°, 所以tan∠EBA=tan∠FAE=
设AF∩BE=P,因为∠PAE+∠PAB=90°,故∠PBA+∠PAB=90° 则∠APB=90°,即EB⊥AF.…(12分) 又因为EB∩BC=B,所以AF⊥平面EBC.…(13分) |
题目简介
如图,四边形ABCD为正方形,EA⊥平面ABCD,EF∥AB,AB=4,AE=2,EF=1.(Ⅰ)求证:BC⊥AF;(Ⅱ)若点M在线段AC上,且满足CM=14CA,求证:EM∥平面FBC;(Ⅲ)试判断
题目详情
(Ⅰ)求证:BC⊥AF;
(Ⅱ)若点M在线段AC上,且满足CM=
(Ⅲ)试判断直线AF与平面EBC是否垂直?若垂直,请给出证明;若不垂直,请说明理由.