 证明:( I)∵四边形ABCD和ABEF都是正方形, ∴AB⊥AF,AB⊥AD, 又AF∩AD=A, ∴AB⊥平面ADF. ∵AB∥EF, ∴EF⊥平面ADF. ∵AM?平面ADF, ∴AM⊥EF. ∵AD=AF,在△ADF中,M是DF的中点, ∴AM⊥DF. 又∵DF∩EF=F, ∴AM⊥平面CDFE. (II)由四边形ABCD和ABEF都是正方形, ∴AB∥EF,AB=EF,AB∥CD,AB=CD, ∴EF∥CD,EF=CD. ∴四边形CDFE为平行四边形, ∴DF∥CE. 又∵DF?平面BCE,CE?平面BCE, ∴DF∥平面BCE. |
题目简介
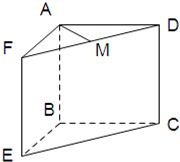
如图所示,四边形ABCD和ABEF都是正方形,点M是DF的中点.(I)求证:AM⊥平面CDFE;(II)求证:DF∥平面BCE.-数学
题目详情
(I)求证:AM⊥平面CDFE;
(II)求证:DF∥平面BCE.