证明:(1):(1)∵E、P分别为AC、A′C的中点,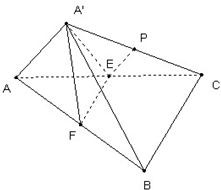 ∴EP∥A′A,又A′A?平面AA′B,而EP?平面AA′B, ∴故有 EP∥平面A′FB. (2)∵E、F分别为直角三角形ABC的直角边AC和斜边AB的中点, ∴EF∥BC. ∵BC⊥AC,EF⊥AE,故EF⊥A′E,∴BC⊥A′E. 而A′E与AC相交,∴BC⊥平面A′EC. 又BC?平面A′BC,∴平面A′BC⊥平面A′EC. |
证明:(1):(1)∵E、P分别为AC、A′C的中点, ∴EP∥A′A,又A′A?平面AA′B,而EP?平面AA′B, ∴故有 EP∥平面A′FB. (2)∵E、F分别为直角三角形ABC的直角边AC和斜边AB的中点, ∴EF∥BC. ∵BC⊥AC,EF⊥AE,故EF⊥A′E,∴BC⊥A′E. 而A′E与AC相交,∴BC⊥平面A′EC. 又BC?平面A′BC,∴平面A′BC⊥平面A′EC. |
题目简介
如图,E、F分别为直角三角形ABC的直角边AC和斜边AB的中点,沿EF将△AEF折起到△A′EF的位置,连接A′B、A′C,P为A′C的中点.(1)求证:EP∥平面A′FB.(2)求证:平面A′EC⊥
题目详情
(1)求证:EP∥平面A′FB.
(2)求证:平面A′EC⊥平面A′BC.