 (1)连接EF,FG, ∵E、F、G分别是AB、BC、CD的中点, ∴FG∥BD, 又∵FG?面EFG,BD?面EFG. ∴BD∥面EFG. (2)由(1),∵E、F、G分别是AB、BC、CD的中点, ∴FE∥AC, 又∵FE?面EFG,AC?面EFG. ∴AC∥面EFG. |
 (1)连接EF,FG, ∵E、F、G分别是AB、BC、CD的中点, ∴FG∥BD, 又∵FG?面EFG,BD?面EFG. ∴BD∥面EFG. (2)由(1),∵E、F、G分别是AB、BC、CD的中点, ∴FE∥AC, 又∵FE?面EFG,AC?面EFG. ∴AC∥面EFG. |
题目简介
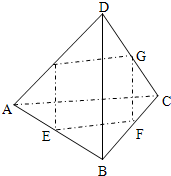
如图,空间四边形ABCD中,E,F,G分别是AB,BC,CD的中点,求证:(1)BD∥平面EFG;(2)AC∥平面EFG.-数学
题目详情
(1)BD∥平面EFG;
(2)AC∥平面EFG.