已知直角梯形ABCD中，AB∥CD，AB⊥BC，AB=1，BC=2，CD=1+3，过A作AE⊥CD，垂足为E，G，F分别为AD，CE的中点，现将△ADE沿AE折叠，使得DE⊥EC．（Ⅰ）求证：BC⊥平

题目简介

已知直角梯形ABCD中，AB∥CD，AB⊥BC，AB=1，BC=2，CD=1+

，过A作AE⊥CD，垂足为E，G，F分别为AD，CE的中点，现将△ADE沿AE折叠，使得DE⊥EC．
（Ⅰ）求证：BC⊥平面CDE；
（Ⅱ）求证：FG∥平面BCD；
（Ⅲ）在线段AE上找一点R，使得面BDR⊥面DCB，并说明理由． 360优课网

题型：解答题难度：中档来源：不详

（I）如下图所示：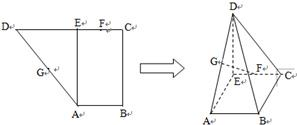

由已知得：DE⊥AE，DE⊥EC
∴DE⊥面ABCE．
∴DE⊥BC，又BC⊥CE，
∴BC⊥面DCE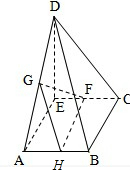
360优课网

（II）取AB中点H，连接GH，FH，
∴GH∥BD，FH∥BC，
∴GH∥面BCD，FH∥面BCD．
∴面FHG∥面BCD，
∴GF∥面BCD．
（III）分析可知，R点满足3AR=RE时，面BDR⊥面BDC．
理由如下：取BD中点Q，连接DR、BR、CR、CQ、RQ
容易计算CD=2，BD=2

，CR=

，DR=

，CQ=

，

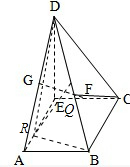在△BDR中
∵BR=

，DR=

，BD=2

，可知RQ=

，
∴在△CRQ中，CQ2+RQ2=CR2，
∴CQ⊥RQ．
又在△CBD中，CD=CB，Q为BD中点
∴CQ⊥BD，
∴CQ⊥面BDR，
∴面BDC⊥面BDR．