 (Ⅰ)证明:因为平面ABCD⊥平面ADEF,∠ADE=90°, 所以DE⊥平面ABCD,(1分) 所以DE⊥AC. 因为ABCD是正方形, 所以AC⊥BD,(3分) 所以AC⊥平面BDE.(4分) (Ⅱ)证明:设AC∩BD=O,取BE中点G,连结FG,OG, 所以,OG∥DE,DE=
因为AF∥DE,DE=2AF,所以AF∥OG且AF=OG, 从而四边形AFGO是平行四边形,FG∥AO.(6分) 因为FG?平面BEF,AO?平面BEF,(7分) 所以AO∥平面BEF,即AC∥平面BEF.(8分) |
题目简介
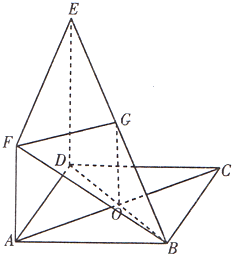
如图所示,正方形ABCD与直角梯形ADEF所在平面互相垂直,∠ADE=90°,AF∥DE,DE=DA=2AF.(Ⅰ)求证:AC⊥平面BDE;(Ⅱ)求证:AC∥平面BEF.-数学
题目详情
(Ⅰ)求证:AC⊥平面BDE;
(Ⅱ)求证:AC∥平面BEF.