 1、过点P作PQ∥AB, ∵AB∥CD, ∴PQ∥AB∥CD, ∴∠PAB+∠1=180°,∠2+∠PCD=180°, ∵∠APC=∠1+∠2, ∴∠APC+∠PAB+∠PCD=∠PAB+∠1+∠2+∠PCD=360°; 2、过点P作PQ∥AB, ∵AB∥CD, ∴PQ∥AB∥CD, ∴∠1=∠PAB,∠2=∠PCD, ∵∠APC=∠1+∠2=∠PAB+∠PCD, ∴∠APC=∠PAB+∠PCD; 3、∵AB∥CD, ∴∠1=∠PCD, ∵∠1=∠PAB+∠APC, ∴∠PCD=∠PAB+∠APC; 4、∵AB∥CD, ∴∠1=∠PAB, ∵∠1=∠PCD+∠APC, ∴∠PAB=∠PCD+∠APC. 故答案为:1.∠APC+∠PAB+∠PCD=360°;2.∠APC=∠PAB+∠PCD;3.∠PCD=∠PAB+∠APC;②;两直线平行,内错角相等. |
题目简介
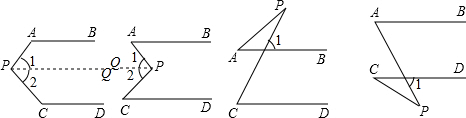
已知AB∥CD,分别探讨下列四个图形中∠APC和∠PAB、∠PCD的关系,并说明其中的一个等式成立的理由.1.______2.______3.______4.∠PAB=∠APC+∠PCD我选择第___
题目详情
1.______2.______3.______4.∠PAB=∠APC+∠PCD
我选择第______个说明理由.理由如下:______.