首页 > 如图，在△ABC中，AC=BC，∠B=30°，D是AC的中点，E是线段BC延长线上一动点，过点A作AF∥BE，与线段ED的延长线交于点F，连接AE、CF．（1）求证：AF=CE；（2）若CE=12BC

如图，在△ABC中，AC=BC，∠B=30°，D是AC的中点，E是线段BC延长线上一动点，过点A作AF∥BE，与线段ED的延长线交于点F，连接AE、CF．（1）求证：AF=CE；（2）若CE=12BC

题目简介

如图，在△ABC中，AC=BC，∠B=30°，D是AC的中点，E是线段BC延长线上一动点，过点A作AF∥BE，与线段ED的延长线交于点F，连接AE、CF．（1）求证：AF=CE；（2）若CE=12BC

题目详情

如图，在△ABC中，AC=BC，∠B=30°，D是AC的中点，E是线段BC延长线上一动点，过点A作AF∥BE，与线段ED的延长线交于点F，连接AE、CF．
（1）求证：AF=CE；
（2）若CE=
1
2
BC，试判断四边形AFCE是什么样的四边形，并证明你的结论；
（3）若CE=BC，求证：EF⊥AC．360优课网
题型：解答题难度：中档来源：不详

答案

（1）证明：∵AF∥BE，
∴∠FAD=∠ECD，∠AFD=∠CED，
在△ADF和△CDE中，
∠FAD=∠ECD
∠AFD=∠CED
AD=CD
，
∴△ADF≌△CDE，
∴AF=CE．

（2）四边形AFCE是矩形．
证明：∵AF∥BE，AF=CE，
∴四边形AFCE是平行四边形．
∴AD=DC，ED=DF．
∵AC=BC，
∴∠BAC=∠B=30°，
∴∠ACE=60°．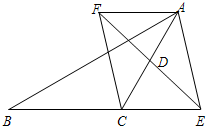
360优课网

∵CE=class="stub"1
2
BC，CD=class="stub"1
2
AC，
∴CE=CD，
∴△DCE为等边三角形，
∴CD=ED，
∴AC=EF，
∴四边形AFCE是矩形．

（3）证明：∵CE=BC，BC=AC，
∴CE=AC．
∵∠ACE=60°，
∴△ACE为等边三角形，∴CE=AE．
∵四边形AFCE是平行四边形，
∴四边形AFCE是菱形．
∴EF⊥AC．

更多内容推荐

Copyright © 2018-2020 360优课网