如图所示，点P是正方形ABCD的对角线BD上一点，PE⊥BC于E，PF⊥CD于F，连接EF，给出下列四个结论：①AP=EF；②△APD一定是等腰三角形；③∠PFE=∠BAP；④PD=2EC，其中正确结

题目简介

如图所示，点P是正方形ABCD的对角线BD上一点，PE⊥BC于E，PF⊥CD于F，连接EF，给出下列四个结论：
①AP=EF； ②△APD一定是等腰三角形； ③∠PFE=∠BAP； ④PD=

EC，
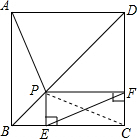
其中正确结论的序号是______． 360优课网

题型：填空题难度：中档来源：不详

如图，连接PC，在正方形ABCD中，∠ABP=∠CBP=45°，AB=CB，
∵在△ABP和△CBP中，

AB=CB

∠ABP=∠CBP

BP=BP

，
∴△ABP≌△CBP（SAS），
∴AP=PC，∠BAP=∠BCP，
又∵PE⊥BC，PF⊥CD，
∴四边形PECF是矩形，
∴PC=EF，∠BCP=∠PFE，
∴AP=EF，∠PFE=∠BAP，故①③正确；
∵PF⊥CD，∠BDC=45°，
∴△PDF是等腰直角三角形，
∴PD=

PF，
又∵矩形的对边PF=EC，
∴PD=

EC，故④正确；
只有点P为BD的中点或PD=AD时，△APD是等腰三角形，故②错误；
综上所述，正确的结论有①③④．
故答案为：①③④．