| 证明: 证法一:∵在梯形ABCD中,AD∥BC,又∵EF=AD, ∴四边形AEFD是平行四边形.(1分) ∴AD∥DF,∴∠AEF=∠DFC.(1分) ∵AB=CD,∴∠B=∠C.(1分) 又∵BE=CF,∴△ABE≌△DCF.(1分) ∴∠AEB=∠DFC,(1分) ∴∠AEB=∠AEF.(1分) ∵∠AEB+∠AEF=180°,∴∠AEF=90°.(1分) ∴四边形AEFD是矩形.(1分) 证法二:连接AF、DE.(1分) 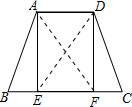 ∵在梯形ABCD中,AD∥BC,又∵EF=AD, ∴四边形AEFD是平行四边形.(1分) ∵AB=CD,∴∠B=∠C.(1分) ∵BE=CF,∴BE+EF=CF+EF,即BF=CE,(1分) ∴△ABF≌△DCE.(1分) ∴AF=DE,(2分) ∴四边形AEFD是矩形.(1分) |
题目简介
已知:如图,在梯形ABCD中,AD∥BC,AB=CD,点E、F在边BC上,BE=CF,EF=AD.求证:四边形AEFD是矩形.-数学
题目详情
求证:四边形AEFD是矩形.