 证明:∵AB=AC, ∴∠B=∠ACB, ∵AE是∠BAC的外角平分线, ∴∠FAE=∠EAC, ∵∠B+∠ACB=∠FAE+∠EAC, ∴∠B=∠ACB=∠FAE=∠EAC, ∴AE∥CD, 又∵DE∥AB, ∴四边形AEDB是平行四边形, ∴AE平行且等于BD, 又∵BD=DC,∴AE平行且等于DC, 故四边形ADCE是平行四边形, 又∵∠ADC=90°, ∴平行四边形ADCE是矩形. 即四边形ADCE是矩形. |
 证明:∵AB=AC, ∴∠B=∠ACB, ∵AE是∠BAC的外角平分线, ∴∠FAE=∠EAC, ∵∠B+∠ACB=∠FAE+∠EAC, ∴∠B=∠ACB=∠FAE=∠EAC, ∴AE∥CD, 又∵DE∥AB, ∴四边形AEDB是平行四边形, ∴AE平行且等于BD, 又∵BD=DC,∴AE平行且等于DC, 故四边形ADCE是平行四边形, 又∵∠ADC=90°, ∴平行四边形ADCE是矩形. 即四边形ADCE是矩形. |
题目简介
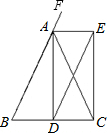
已知:如图,△ABC中,AB=AC,AD是BC边上的高,AE是△BAC的外角平分线,DE∥AB交AE于点E,求证:四边形ADCE是矩形.-数学
题目详情