（下面提供两题备选，请在a、b中选择一道你所熟悉的题进行解答）a、如图1，在平行四边形ABCD中，E是AD的中点，CE与BA的延长线相交于F点．连结DF．（1）求证：四边形ACDF是平行四边形-数学

题目简介

题目详情

（下面提供两题备选，请在a、b中选择一道你所熟悉的题进行解答）

360优课网

a、如图1，在平行四边形ABCD中，E是AD的中点，CE与BA的延长线相交于F点．连结DF．
（1）求证：四边形ACDF是平行四边形．
（2）若ACDF是矩形，试探求∠1与∠2之间的关系．
b、如图2，等腰梯形ABCD中，E、F是两腰的中点，连接线段AF，作EG∥AF，交BC于G，再连结线段FG．
（1）求证：四边形AEGF是平行四边形．
（2）若AEGF是矩形，试探求∠1与∠2之间的关系．

题型：解答题难度：中档来源：不详

答案

a、如图1．
（1）证明：∵平行四边形ABCD中，E是AD的中点，
∴AE=ED，BF∥CD，
∴∠FAE=∠CDE．
在△AEF与△DEC中，

∠FAE=∠CDE

AE=DE

∠AEF=∠DEC

，
∴△AEF≌△DEC，
∴AF=CD，
又BF∥CD，即AF∥CD，
∴四边形ACDF是平行四边形；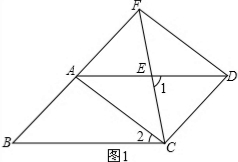

360优课网

（2）∠1=2∠2．理由如下：
∵ACDF是矩形，
∴AE=CE，
∴∠EAC=∠ECA，
又∵平行四边形ABCD中，AD∥BC，
∴∠EAC=∠2，
∴∠EAC=∠ECA=∠2，
∴∠1=∠EAC+∠ECA=∠2+∠2=2∠2．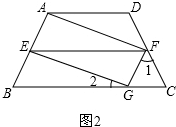

360优课网

b、如图2．
（1）证明：∵等腰梯形ABCD中，E、F是两腰的中点，
∴EF为梯形ABCD的中位线，
∴EF∥BC，
又∵EG∥AF，
∴∠AFE=∠FEG=∠2，∠BAF=∠BEG．
在△AEF与△EBG中，

∠AFE=∠2

∠EAF=∠BEG

AE=EB

，
∴△AEF≌△EBG，
∴AF=EG，
∵AF∥EG，
∴四边形AEGF是平行四边形；

（2）∠1=2∠2．理由如下：
理由是：∵AEGF是矩形，
∴FG∥AB，∠AEG=∠EGF=90°，
∴∠B=∠C=∠FGC，
∵∠2+∠B=90°，2∠B+∠1=180°，
∴2∠B+∠1=2（∠2+∠B）=180°，
∴∠1=2∠2．

上一篇 : 已知正方形ABCD，GE⊥BD于B，AG⊥G
下一篇 : 已知矩形一条对角线与一边的夹

（下面提供两题备选，请在a、b中选择一道你所熟悉的题进行解答）a、如图1，在平行四边形ABCD中，E是AD的中点，CE与BA的延长线相交于F点．连结DF．（1）求证：四边形ACDF是平行四边形-数学

题目简介

题目详情

答案

更多内容推荐