已知矩形ABCD中，对角线AC、BD相交于点O，E、F是对角线BD上的两点，且BF=DE．（1）按边分类，△AOB是______三角形；（2）猜想线段AE、CF的大小关系，并证明你的猜想．-数学

题目简介

题目详情

已知矩形ABCD中，对角线AC、BD相交于点O，E、F是对角线BD上的两点，且BF=DE．
（1）按边分类，△AOB是______三角形；
（2）猜想线段AE、CF的大小关系，并证明你的猜想． 360优课网

题型：解答题难度：中档来源：百色

答案

（1）等腰；
理由：由于矩形的对角线相等且互相平分，所以OA=OB，即△AOB是等腰三角形．

（2）猜想：AE=CF；
证法一：∵四边形ABCD是矩形，
∴AD∥BC，且AD=BC，
∴∠ADB=∠CBD，
∵DE=BF，
∴△ADE≌△CBF（SAS），
∴AE=CF．
证法二：∵四边形ABCD是矩形，
∴OA=OC，OB=OD，
∵DE=BF，∴OE=OF，
又∠AOE=∠COF，
∴△AOE≌△COF（SAS），
∴AE=CF．
证法三：如图，连接AF、CE，
由四边形ABCD是矩形得OA=OC，OB=OD，
∵DE=BF，∴OE=OF，
∴四边形AECF是平行四边形，
∴AE=CF．

上一篇 : 如图，四边形ABCD、DEBF都是矩形
下一篇 : 矩形两条对角线的夹角为60°，一

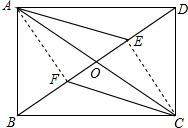
已知矩形ABCD中，对角线AC、BD相交于点O，E、F是对角线BD上的两点，且BF=DE．（1）按边分类，△AOB是______三角形；（2）猜想线段AE、CF的大小关系，并证明你的猜想．-数学

题目简介

题目详情

答案

更多内容推荐