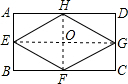
 连接EH、HF,如右图所示: ∵E、F、G、H分别是矩形ABCD的四条边的中点, ∴HF∥AB∥DC,EG∥AD∥BC, 即:HF⊥EG, EG=BC=4,HF=AB=2, EH2=EF2=FG2=GH2=(
∴四边形EHGF是菱形, ∴SEFGH=
故选A. |
 连接EH、HF,如右图所示: ∵E、F、G、H分别是矩形ABCD的四条边的中点, ∴HF∥AB∥DC,EG∥AD∥BC, 即:HF⊥EG, EG=BC=4,HF=AB=2, EH2=EF2=FG2=GH2=(
∴四边形EHGF是菱形, ∴SEFGH=
故选A. |
题目简介
如图,在矩形ABCD中,E、F、G、H分别是四条边的中点,AB=2,BC=4,则四边形EFGH的面积为()A.4B.6C.3D.8-数学
题目详情