证明:如图∵矩形ABCD中,AB=CD,AD=BC,AB:BC=5:6,EC=
∴DF=
∴
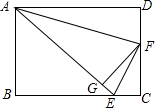 ∴
又∵∠ECF=∠FDF, ∴△CEF∽△DFA,
∴∠AFD+∠CFE=∠FEC+∠CFE=90°, ∴∠AFE=90°. 又∵FG⊥AE, ∴△AFE∽△AGF,△AFG∽△FEG, ∴
∴AG=4EG. |
证明:如图∵矩形ABCD中,AB=CD,AD=BC,AB:BC=5:6,EC=
∴DF=
∴
 ∴
又∵∠ECF=∠FDF, ∴△CEF∽△DFA,
∴∠AFD+∠CFE=∠FEC+∠CFE=90°, ∴∠AFE=90°. 又∵FG⊥AE, ∴△AFE∽△AGF,△AFG∽△FEG, ∴
∴AG=4EG. |
题目简介
已知:如图,矩形ABCD中AB:BC=5:6,点E在BC上,点F在CD上,EC=16BC,FC=35CD,FG⊥AE与G.求证:AG=4GE.-数学
题目详情