 如右图所示,连接MN、FP,并延长FP交AD于Q, ∵四边形ABCD是矩形, ∴AB=CD,AB∥CD, ∴∠PDG=∠PEA,∠PGD=∠PAE, 又∵E、G是AB、CD中点, ∴AE=
∴AE=DG, ∴△PDG≌△PEA, ∴PD=PE,PG=PA, ∴P是DE、AG中点, 又∵F是BC中点, ∴PF∥CD, ∴FQ∥CD, ∴△DQP∽△DAE, ∴QP:AE=DQ:AD=1:2, ∴PQ=
∴PQ=
∴四边形ABFQ、FCDQ是矩形, ∵F是BC中点, ∴AQ=DQ=BF=CF, ∴PF=
∵AB∥PQ, ∴△AEM∽△FPM, ∴AM:MF=AE:PF=3:2, 同理DN:NF=3:2, ∴AM:MF=DN:NF, ∴MN∥AD, ∴MN⊥FQ, ∴MN:AD=MF:AF=3:5, ∴MN=
∴S四边形MFNP=
故答案为:9. |
题目简介
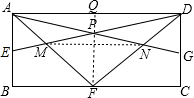
如图,在长方形ABCD中,E、F、G分别是边AB、BC、CD的中点.已知长方形ABCD的面积是40cm2.则四边形MFNP的面积是______cm2.-数学
题目详情