如图，已知矩形ABCD的边长AB=2，BC=3，点P是AD边上的一动点，P异于A、D，Q是BC边上的一动点，连接AQ、DQ，过P作PE∥DQ交AQ于E，作PF∥AQ交DQ于F．（1）请你判断△APE与

题目简介

题目详情

如图，已知矩形ABCD的边长AB=2，BC=3，点P是AD边上的一动点，P异于A、D，Q是BC边上的一动点，连接AQ、DQ，过P作PE∥DQ交AQ于E，作PF∥AQ交DQ于F．
（1）请你判断△APE与△PDF的关系，并说明理由；
（2）若Q是BC的中点，当P点运动到什么位置时，四边形PEQF为菱形？说明理由． 360优课网

题型：解答题难度：中档来源：不详

答案

（1）△APE∽△PDF．
理由：∵PE∥DQ，PF∥AQ，
∴∠APE=∠PDF，∠PAE=∠DPF，
∴△APE∽△PDF；

（2）当P运动到AD中点时，四边形PEQF是菱形．
理由：∵PE∥DQ，PF∥AQ，
∴四边形PEQF是平行四边形，
∵Q是BC的中点，
∴BQ=CQ，
∵四边形ABCD是矩形，
∴AB=CD，∠B=∠C=90°，
在△ABQ和△DCQ中，

AB=DC

∠B=∠C

BQ=CQ

，
∴△ABQ≌△DCQ（SAS），
∴AQ=DQ，
∴∠PAE=∠PDF，
∵∠PDF=∠APE，
∴∠PAE=∠APE，
∴PE=AE，
∵△APE∽△PDF，
∴AE：PF=AP：PD，
∵AP=PD，
∴AE=PF，
∴PE=PF，
∴四边形PEQF是菱形．

上一篇 : 如图为长方形时钟钟面示意图，时
下一篇 : 如图是一块电脑主板，每一个转角

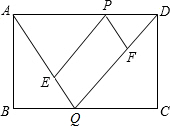
如图，已知矩形ABCD的边长AB=2，BC=3，点P是AD边上的一动点，P异于A、D，Q是BC边上的一动点，连接AQ、DQ，过P作PE∥DQ交AQ于E，作PF∥AQ交DQ于F．（1）请你判断△APE与

题目简介

题目详情

答案

更多内容推荐