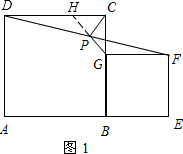
 (1)如图1,当点A,B,E在同一条直线上时,有结论:PG⊥PC,PG=PC. 延长GP交DC与点H. ∵P是线段DF的中点, ∴FP=DP. 由题意知DC∥AE, ∴∠GFP=∠HDP, ∵∠GPF=∠HPD, ∴△GFP≌△HDP, ∴GP=HP,GF=HD, ∵四边形ABCD、BEFG是正方形, ∴CD=CB,GB=GF. ∴CH=CG, 又∵∠HCG=90°,GP=HP, ∴PG⊥PC,PG=PC; (2)如图2,当点A,B,E在同一条直线上时,有结论:PG⊥PC,PG=PC 延长GP交DC延长线于点H. 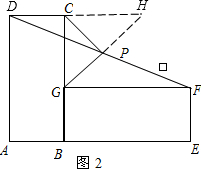 ∵P是线段DF的中点, ∴FP=DP. 由题意可知DC∥GF, ∴∠GFP=∠HDP, ∵∠GPF=∠HPD, ∴△GFP≌△HDP, ∴GP=HP,GF=HD, ∵矩形ABCD≌矩形BEFG, ∴CD=GB,CB=GF, ∴CH=CG 又∵∠HCG=90°,GP=HP, ∴PG⊥PC,PG=PC. |
题目简介
问题:如图,在正方形ABCD和正方形BEFG中,点A,B,E在同一条直线上,P是线段DF的中点,连接PG,PC.试探究PG与PC的位置关系及PGPC的值.小聪同学的思路是:延长GP交DC于点H,构-数
题目详情
交DC于点H,构造全等三角形,经过推理使问题得到解决.
请你参考小聪同学的思路,探究并解决下列问题:
(1)写出上面问题中线段PG与PC的位置关系及
(2)若将条件“正方形ABCD和正方形BEFG”改为“矩形ABCD≌矩形BEFG”其它条件不变,画图试探求线段PG与PC的关系.