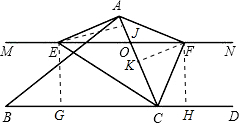
 (1)如图所示:作EG⊥BC,EJ⊥AC,FK⊥AC,FH⊥BC, 因为直线EC,CF分别平分∠ACB与∠ACD,所以EG=EJ,FK=FH, 在△EJO与△FKO中,
所以△EJO≌△FKO,即OE=OF(3分) (2)当OA=OC,OE=OF时,四边形AECF是矩形, 证明:∵OA=OC,OE=OF, ∴四边形AECF为平行四边形, 又∵直线MN与∠BCA的平分线相交于点E,与∠DCA(△ABC的外角)的平分线相交于点F. ∴∠ACE=∠BCE,∠ACF=∠FCD, 由∠BCE+∠ACE+∠ACF+∠FCD=180°, ∴∠ECA+∠ACF=90°,即∠ECF=90°, ∴四边形AECF为矩形;(3分) (3)由(2)可知,四边形AECF是矩形,要使其为正方形,再加上对角线垂直即可,即∠ACB=90°(10分) |
题目简介
如图,在△ABC中,点O是AC边上的一个动点(点O不与A、C两点重合),过点O作直线MN∥BC,直线MN与∠BCA的平分线相交于点E,与∠DCA(△ABC的外角)的平分线相交于点F.(1)OE与OF相
题目详情
(1)OE与OF相等吗?为什么?
(2)探究:当点O运动到何处时,四边形AECF是矩形?并证明你的结论.
(3)在(2)中,当∠ACB等于多少时,四边形AECF为正方形.(不要求说理由)