 (1)证明: ∵AD∥BC, ∴∠DAE=∠F,∠ADE=∠FCE. ∵E为CD的中点, ∴ED=EC. ∴△ADE≌△FCE(AAS). ∴EF=EA.(5分) (2)连接GA, ∵AD∥BC,∠ABC=90°, ∴∠DAB=90°. ∵DG⊥BC, ∴四边形ABGD是矩形. ∴BG=AD,GA=BD. ∵BD=BC, ∴GA=BC. 由(1)得△ADE≌△FCE, ∴AD=FC. ∴GF=GC+FC=GC+AD=GC+BG=BC=GA. ∵由(1)得EF=EA, ∴EG⊥AF.(5分) |
 (1)证明: ∵AD∥BC, ∴∠DAE=∠F,∠ADE=∠FCE. ∵E为CD的中点, ∴ED=EC. ∴△ADE≌△FCE(AAS). ∴EF=EA.(5分) (2)连接GA, ∵AD∥BC,∠ABC=90°, ∴∠DAB=90°. ∵DG⊥BC, ∴四边形ABGD是矩形. ∴BG=AD,GA=BD. ∵BD=BC, ∴GA=BC. 由(1)得△ADE≌△FCE, ∴AD=FC. ∴GF=GC+FC=GC+AD=GC+BG=BC=GA. ∵由(1)得EF=EA, ∴EG⊥AF.(5分) |
题目简介
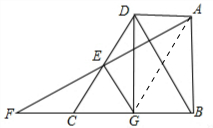
如图,在直角梯形ABCD中,AD∥BC,∠ABC=90°,BD=BC,E为CD的中点,交BC的延长线于F;(1)证明:EF=EA;(2)过D作DG⊥BC于G,连接EG,试证明:EG⊥AF.-数学
题目详情
(1)证明:EF=EA;
(2)过D作DG⊥BC于G,连接EG,试证明:EG⊥AF.