| 证明:(1)∵BC=2AD,点E是BC的中点, ∴EC=AD. ∵AD∥BC, ∴∠ADO=∠CEO,∠DAO=∠ECO. 在△AOD和△COE中
∴△AOD≌△COE(ASA); (2)∵AD=BE,AD∥BE, ∴四边形ABED是平行四边形; 同理可得:四边形AECD是平行四边形. 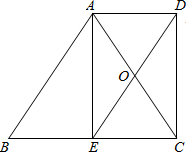 ∴∠ADO=∠B. ∵∠B=
∴∠AOE=2∠B. ∴∠AOE=2∠ADO. ∵∠AOE=∠ADO+∠DAO, ∴∠OAD=∠ODA. ∴OA=OD. ∴AC=DE. ∴四边形AECD是矩形. |
| 证明:(1)∵BC=2AD,点E是BC的中点, ∴EC=AD. ∵AD∥BC, ∴∠ADO=∠CEO,∠DAO=∠ECO. 在△AOD和△COE中
∴△AOD≌△COE(ASA); (2)∵AD=BE,AD∥BE, ∴四边形ABED是平行四边形; 同理可得:四边形AECD是平行四边形.  ∴∠ADO=∠B. ∵∠B=
∴∠AOE=2∠B. ∴∠AOE=2∠ADO. ∵∠AOE=∠ADO+∠DAO, ∴∠OAD=∠ODA. ∴OA=OD. ∴AC=DE. ∴四边形AECD是矩形. |
题目简介
如图,在梯形ABCD中,AD∥BC,BC=2AD,点E是BC的中点,连接AC、DE相交于点O.(1)试说明:△AOD≌△COE;(2)若∠B=12∠AOE,试说明四边形AECD是矩形的理由.-数学
题目详情
(1)试说明:△AOD≌△COE;
(2)若∠B=