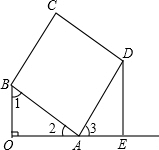
 (1)证明:如图所示, ∵OA⊥OB, ∴∠1+∠2=90°, 又∵四边形ABCD是矩形, ∴∠BAD=90°, ∴∠2+∠3=90°, ∴∠1=∠3,(1分) ∵OA⊥OB,OE⊥OA, ∴∠BOA=∠DEA=90°,(2分) ∴△OAB∽△EDA.(3分) (2)在Rt△OAB中,AB=
由(1)可知∠1=∠3,∠BOA=∠DEA=90°, ∴当a=AD=AB=5时,△AOB与△EDA全等.(5分) 当a=AD=AB=5时,可知矩形ABCD为正方形, ∴BC=AB,如图,过点C作CH⊥OE交OE于点H, 则CH就是点C到OE的距离,过点B作BF⊥CH交CH于点F, 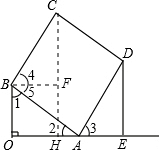 则∠4与∠5互余,∠1与∠5互余, ∴∠1=∠4,(6分) 又∵∠BFC=∠BOA,BC=AB, ∴△OAB≌△FCB(AAS),(7分) ∴CF=OA=4,BO=BF. ∴四边形OHFB为正方形, ∴HF=OB=3, ∴点C到OE的距离CH=CF+HF=4+3=7.(8分) |
题目简介
如图,已知OA⊥OB,OA=4,OB=3,以AB为边作矩形ABCD,使AD=a,过点D作DE垂直OA的延长线交于点E.(1)证明:△OAB∽△EDA;(2)当a为何值时,△OAB与△EDA全等?请说明
题目详情
长线交于点E.
(1)证明:△OAB∽△EDA;
(2)当a为何值时,△OAB与△EDA全等?请说明理由,并求出此时点C到OE的距离.