首页 > 如图，点P是正方形ABCD的对角线BD上一点，PE⊥BC于点E，PF⊥CD于点F，连接EF给出下列五个结论：①AP=EF；②AP⊥EF；③△APD一定是等腰三角形；④∠PFE=∠BAP；⑤PD=EC．

如图，点P是正方形ABCD的对角线BD上一点，PE⊥BC于点E，PF⊥CD于点F，连接EF给出下列五个结论：①AP=EF；②AP⊥EF；③△APD一定是等腰三角形；④∠PFE=∠BAP；⑤PD=EC．

题目简介

如图，点P是正方形ABCD的对角线BD上一点，PE⊥BC于点E，PF⊥CD于点F，连接EF给出下列五个结论：①AP=EF；②AP⊥EF；③△APD一定是等腰三角形；④∠PFE=∠BAP；⑤PD=EC．

题目详情

如图，点P是正方形ABCD的对角线BD上一点，PE⊥BC于点E，PF⊥CD于点F，连接EF给出下列五个结论：
①AP=EF；②AP⊥EF；③△APD一定是等腰三角形；④∠PFE=∠BAP；⑤PD=EC．
其中正确结论的序号是______．360优课网
题型：填空题难度：中档来源：吉林模拟

答案


360优课网
过点P作PN⊥AB，垂足为点N，延长AP，交EF于点M，
∵四边形ABCD是正方形，
∴∠ABP=∠CBD=45°，
∴△DFP为等腰直角三角形，
∴DF=PF，又AN=DF，
∴AN=FP，
又∵NP⊥AB，PE⊥BC，
∴四边形BNPE是正方形，
∴NP=EP，
又∵AP=PC，
四边形PECF为矩形，∴EF=PC，
∴AP=EF，故①正确；
在△ANP≌△FPE中
AN=FP
NP=EP
AP=EF

则△ANP≌△FPE（SSS），
∴∠PFE=∠BAP，故④正确；
△APN与△FPM中，∠APN=∠FPM，∠NAP=∠PFM
∴∠PMF=∠ANP=90°
∴AP⊥EF，故②正确；
P是BD上任意一点，因而△APD不一定是等腰三角形，故③错误；
∵在Rt△PDF中，PD＞PF，
在矩形PECF中，PF=EC，
∴PD＞EC，故⑤错误；
故答案为：①②④．

更多内容推荐

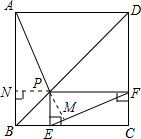
Copyright © 2018-2020 360优课网