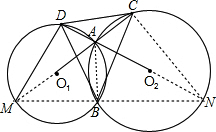
 证明:设两圆为⊙O、⊙Q,如图 延长CA交⊙O1于M点,延长DA交⊙O2于N点,连接AB、DM、CN、MN, ∵AM是⊙O1的直径,AN是⊙O2的直径, ∴∠MDN=∠ACN=90°, ∴C、D、M、N四点共圆, ∴∠DMC=∠DNC, ∵∠DMC=∠DBA,∠DNC=∠ABC, ∴∠DBA=∠ABC, ∴点A在∠DBC的角平分线上, ∵C、D、M、N四点共圆, ∴∠DCM=∠DNM, ∵∠DNM=∠ACB, ∴∠DCM=∠ACB, ∴点A在∠DCB的角平分线上, 同理:点A在∠CDB的角平分线上, ∴点A是△CDB的三个角平分线的交点, ∴点A是△BCD的内心. |
题目简介
⊙O2与⊙O1交于A,B两点,射线O1A交⊙O2于C点,射线O2A交⊙O1于D点.求证:点A是△BCD的内心.-数学
题目详情