首页 > 定理：图1，如果∠ADB=∠ACB，那么四边形ABCD有外接圆，也叫做A，B，C，D四点共圆．（注：本定理不需要证明）（1）图2，△ABC中，AC=BC，点E，F分别在线段AC，BC上运动（不与端点重

定理：图1，如果∠ADB=∠ACB，那么四边形ABCD有外接圆，也叫做A，B，C，D四点共圆．（注：本定理不需要证明）（1）图2，△ABC中，AC=BC，点E，F分别在线段AC，BC上运动（不与端点重

题目简介

定理：图1，如果∠ADB=∠ACB，那么四边形ABCD有外接圆，也叫做A，B，C，D四点共圆．（注：本定理不需要证明）（1）图2，△ABC中，AC=BC，点E，F分别在线段AC，BC上运动（不与端点重

题目详情

定理：图1，如果∠ADB=∠ACB，那么四边形ABCD有外接圆，也叫做A，B，C，D四点共圆．（注：本定理不需要证明）
（1）图2，△ABC中，AC=BC，点E，F分别在线段AC，BC上运动（不与端点重合），而且CE=BF，O是△ABC的外心（外接圆的圆心，它到三角形三个顶点距离相等），试证明C，E，O，F四点共圆．（注：可以使用上述定理，也可以采用其他方法）

360优课网

如果将问题2中的点C“分离”成两个点，那么就有：
（2）图3，在凸四边形ABCD中，AD=BC，点E，F分别在线段AD，BC上运动（不与端点重合），而且DE=BF，直线AC，BD相交于点P，直线EF，BD相交于点Q，直线EF，AC相交于点R．当点E，F分别在线段AD，BC上运动（不与端点重合）时，探究△PQR的外接圆是否经过除点P外的另一个定点？如果是，请给出证明，并指出是哪个定点；如果不是，请说明理由．
题型：解答题难度：中档来源：不详

答案

证明：（1）∵OB=0C，
∴∠OCB=∠OBC，
又∵AC=BC，
∴∠OCB=∠OCA，
∴∠OBC=∠OCA，
在△ECO与△FBO中，
OC=OB
∠ECO=∠FBO
CE=BF
，
∴△ECO≌△FBO，
∴∠EOC=∠FOB，又∠AOC=∠BOC，
∴∠EOF=∠COB，
又∵EO=OF，
∴∠OEF=∠OCF，
∴C，E，O，F四点共圆；

（2）由于是将问题2中的点C“分离”成两个点，
根据图形变换的过程，猜测△PQR的外接圆一定经过线段AC，BD垂直平分线的交点O．
下面给予证明：
显然△ODA≌△OCB，
∴∠OBF=∠ODE，
∴△OBF≌△ODE，
∴OE=OF且∠BOF=∠DOE，
∴∠BOD=∠EOF，
∴△EOF∽△BOD∽△COA，
∴∠OBD=∠OEF=∠OCA，
∴O，B，F，Q四点共圆，O，F，C，R四点也共圆，
∴∠OFB=∠OQB=∠ORP，
∴P，Q，O，R四点共圆，即当点E和F变动时，△PQR的外接圆经过除点P外的另一个定点O．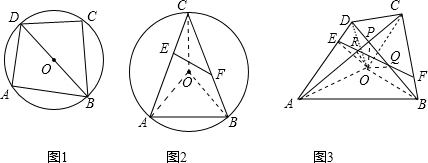

360优课网

更多内容推荐

Copyright © 2018-2020 360优课网