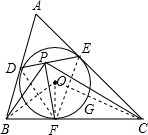
 证明:连接OF,OB,OC,OC交弧EF于G,连接DF,EF, ∵⊙O为△ABC的内切圆, ∴CE=CF,BD=BF,弧FG=
∴∠FDE=∠COF,而∠DPF=∠OFC, ∴△DPF∽△OFC,同理△EPF∽△OFB, ∴
∴OF?PF=PD?CF=PD?CE, OF?PF=PE?BF=PE?BD, ∴PD?CE=PE?BD, ∴
而∠BDP=∠CEP, ∴△BDP∽△CEP, ∴∠DBP=∠ECP. |
 证明:连接OF,OB,OC,OC交弧EF于G,连接DF,EF, ∵⊙O为△ABC的内切圆, ∴CE=CF,BD=BF,弧FG=
∴∠FDE=∠COF,而∠DPF=∠OFC, ∴△DPF∽△OFC,同理△EPF∽△OFB, ∴
∴OF?PF=PD?CF=PD?CE, OF?PF=PE?BF=PE?BD, ∴PD?CE=PE?BD, ∴
而∠BDP=∠CEP, ∴△BDP∽△CEP, ∴∠DBP=∠ECP. |
题目简介
如图,⊙O是△ABC的内切圆,D、E、F是切点,FP⊥DE于P,求证:∠DBP=∠ECP.-数学
题目详情