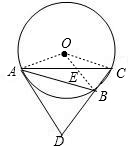
 证明:如图:连接OA,OB,OC,且OB交AC于E, ∵∠ACB=45°,∠ABC=120°,∴∠AOB=90°,∠E0C=∠ECO=∠OAE=30°, 在直角△AOE中,设OE=a,则AE=2a,EC=a, ∴
又∵DB=2BC,∴
∴
∴OB∥AD, ∴∠OAD=∠AOB=90°. 所以AD切⊙O于点A. |
 证明:如图:连接OA,OB,OC,且OB交AC于E, ∵∠ACB=45°,∠ABC=120°,∴∠AOB=90°,∠E0C=∠ECO=∠OAE=30°, 在直角△AOE中,设OE=a,则AE=2a,EC=a, ∴
又∵DB=2BC,∴
∴
∴OB∥AD, ∴∠OAD=∠AOB=90°. 所以AD切⊙O于点A. |
题目简介
如图,已知⊙O是△ABC的外接圆,∠ACB=45°,∠ABC=120°,延长CB到D,使DB=2BC,连接AD,求证:AD切⊙O于点A.-数学
题目详情