△ABC的内切圆分别切BC、CA、AB三边于D、E、F，G是EF上的一点，且DG⊥EF，求证：DG平分∠BGC．-数学

题目简介

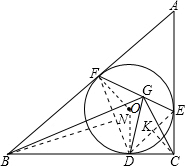
△ABC的内切圆分别切BC、CA、AB三边于D、E、F，G是EF上的一点，且DG⊥EF，求证：DG平分∠BGC． 360优课网

题型：解答题难度：中档来源：不详

证明：连接DF、DE，设N、K分别是DF、DE的中点，连接BN、CK，OF，OD．则：
∵△ABC的内切圆分别切BC、CA、AB三边于D、E、F，
∴BF=BD，CD=CE，
∴BN⊥DF，CK⊥DE，∠FBN=class="stub"1

∠FBD，
∵∠DOF=2∠E，∠DOF+∠FBD=180°，∠GDE+∠E=90°，
∴∠FBN=∠EDG，
∵DG⊥EG，
∴∠BNF=∠DGE=90°，
∴Rt△BFN∽Rt△DEG，class="stub"BF

=class="stub"FN

=class="stub"FD

2GE

（2分）
同理：Rt△CEK∽Rt△DFG，class="stub"CE

=class="stub"EK

=class="stub"ED

2FG

（2分）
∴BF?GE=class="stub"1

DF?DE=CE?FG（4分）
∴class="stub"BF

=class="stub"FG

，而∠BFG=∠CEG（2分）
∴△BFG∽△CEG，于是∠BGF=∠CGE．
∵DG⊥EF，∴∠BGD=∠CGD．
即DG平分∠BGC．