 ∵AB=AD, ∴∠ABD=∠ADB, ∵∠BCD=120°, ∴∠ABD=∠ADB=60°, ∴△ABD是等边三角形; 连接OB,OD,过O作OE⊥BD于E,则∠OBD=30°; ∵OB=8cm, ∴OE=4cm, ∴△ABD的内切圆面积=16π. |
 ∵AB=AD, ∴∠ABD=∠ADB, ∵∠BCD=120°, ∴∠ABD=∠ADB=60°, ∴△ABD是等边三角形; 连接OB,OD,过O作OE⊥BD于E,则∠OBD=30°; ∵OB=8cm, ∴OE=4cm, ∴△ABD的内切圆面积=16π. |
题目简介
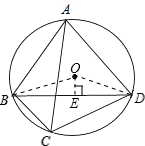
如图,已知四边形ABCD为⊙O的内接四边形,AB=AD,∠BCD=120°,当⊙O的半径为8cm时,求:△ABD的内切圆面积.-数学
题目详情