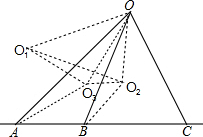
 证明:连接OO1,OO2,OO3,O1O2,O1O3,AO3,BO2, ∵O1,O2,O3分别为△OAB,△OBC,△OCA的外心, ∴O1O2垂直平分OB,O1O3垂直平分OA, 由圆周角定理可得,∠OO2O1=
∴∠OO2O1=∠OO3O1, ∴O,O1,O2,O3共圆. |
 证明:连接OO1,OO2,OO3,O1O2,O1O3,AO3,BO2, ∵O1,O2,O3分别为△OAB,△OBC,△OCA的外心, ∴O1O2垂直平分OB,O1O3垂直平分OA, 由圆周角定理可得,∠OO2O1=
∴∠OO2O1=∠OO3O1, ∴O,O1,O2,O3共圆. |
题目简介
A、B、C三点共线,O点在直线外,O1,O2,O3分别为△OAB,△OBC,△OCA的外心.求证:O,O1,O2,O3四点共圆.-数学
题目详情