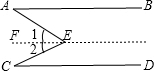
 如图所示, (1)∠AEC=∠A+∠C. 证明:过点E作EF∥AB, ∴∠1=∠A; 又已知AB∥CD, ∴EF∥CD(平行公理), ∴∠2=∠C; 又∵∠AEC=∠1+∠2, ∴∠AEC=∠A+∠C. (2)不成立,结论应是∠A=∠AEC+∠C或∠C=∠AEC+∠A. 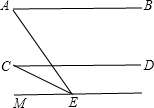 证明:如果E在CD下方,过E作EM∥AB∥CD, 那么可得出∠A=∠AEM,∠C=∠MEC, ∵∠AEM=∠AEC+∠MEC, ∴∠A=∠AEC+∠C, 如果E在AB上方,证法同上,可得出的结论是∠C=∠AEC+∠A. 当点E在点A和点C左侧时∠A+∠AEC+∠C=360°. |
题目简介
如图,AB∥CD,在AB与CD之间任意找一点E,连接AE,CE(说明:AB,CD都为线段),自己画出图形并探索下面问题:(1)试问∠AEC与∠C有何种关系?请猜想并给出证明.(2)当E点在平行线AB,
题目详情
(1)试问∠AEC与∠C有何种关系?请猜想并给出证明.
(2)当E点在平行线AB,CD的外部时,上一问的结论是否仍然成立?画图探索并予以证明.