| 证明:(1)连接OD. ∵AD∥OC, ∴∠BOC=∠OAD,∠COD=∠ODA, 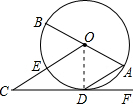 ∵OA=OD, ∴∠OAD=∠ODA. ∴∠BOC=∠COD, ∴
(2)由(1)∠BOC=∠OAD,∠OAD=∠ODA. ∴∠BOC=∠ODA. ∵∠BOC+∠ADF=90°. ∴∠ODA+∠ADF=90°, 即∠ODF=90°. ∵OD是⊙O的半径, ∴CD是⊙O的切线. |
| 证明:(1)连接OD. ∵AD∥OC, ∴∠BOC=∠OAD,∠COD=∠ODA,  ∵OA=OD, ∴∠OAD=∠ODA. ∴∠BOC=∠COD, ∴
(2)由(1)∠BOC=∠OAD,∠OAD=∠ODA. ∴∠BOC=∠ODA. ∵∠BOC+∠ADF=90°. ∴∠ODA+∠ADF=90°, 即∠ODF=90°. ∵OD是⊙O的半径, ∴CD是⊙O的切线. |
题目简介
如图,AB是⊙O的直径,点D在⊙O上,OC∥AD交⊙O于E,点F在CD延长线上,且∠BOC+∠ADF=90°.(1)求证:DE=BE;(2)求证:CD是⊙O的切线.-数学
题目详情
(1)求证:
(2)求证:CD是⊙O的切线.