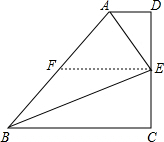
 证明:过E作EF∥BC, ∵E是CD的中点, ∴AF=BF, ∴EF是梯形ABCD的中位线, ∴AD∥EF,EF=
∴∠AEF=∠EAD, ∵AB=AD+BC, ∴AF=EF, ∴∠AEF=∠EAF, ∴∠EAD=∠EAF, ∴AE平分∠BAD, 同理可证得:BE平分∠ABC. |
 证明:过E作EF∥BC, ∵E是CD的中点, ∴AF=BF, ∴EF是梯形ABCD的中位线, ∴AD∥EF,EF=
∴∠AEF=∠EAD, ∵AB=AD+BC, ∴AF=EF, ∴∠AEF=∠EAF, ∴∠EAD=∠EAF, ∴AE平分∠BAD, 同理可证得:BE平分∠ABC. |
题目简介
如图,在梯形ABCD中,AD∥BC,AB=AD+BC,E为CD中点,连接AE、BE,试说明:BE平分∠ABC,AE平分∠BAD.-数学
题目详情