| (1)∵AF⊥平面BDE,BE?平面BDE,AD⊥平面ABE,BE?平面ABE ∴AF⊥BE,AD⊥BE,而AD∩AF=A 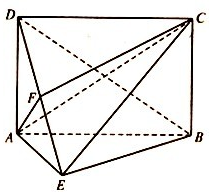 ∴BE⊥平面ADE; (2)设AC与BD交于O,连接FO ∵AD=AE,AF⊥DE ∴点F为DE的中点,而O为BD的中点 根据中位线定理可知BE∥FO 而FO?平面AFC,BE?平面AFC ∴BE∥平面AFC; (3)∵BE⊥平面ADE,BE∥FO ∴FO⊥平面ADE 而FO?平面AFC ∴平面AFC⊥平面ADE. |
| (1)∵AF⊥平面BDE,BE?平面BDE,AD⊥平面ABE,BE?平面ABE ∴AF⊥BE,AD⊥BE,而AD∩AF=A  ∴BE⊥平面ADE; (2)设AC与BD交于O,连接FO ∵AD=AE,AF⊥DE ∴点F为DE的中点,而O为BD的中点 根据中位线定理可知BE∥FO 而FO?平面AFC,BE?平面AFC ∴BE∥平面AFC; (3)∵BE⊥平面ADE,BE∥FO ∴FO⊥平面ADE 而FO?平面AFC ∴平面AFC⊥平面ADE. |
题目简介
如图,已知四边形ABCD是矩形,AD⊥平面ABE,AD=AE,点F在线段DE上,且AF⊥平面BDE.求证:(1)BE⊥平面ADE;(2)BE∥平面AFC;(3)平面AFC⊥平面ADE.-数学
题目详情
(1)BE⊥平面ADE;
(2)BE∥平面AFC;
(3)平面AFC⊥平面ADE.