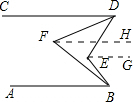
 过点E、F分别作AB的平行线EG、FH,由平行线的传递性可得AB∥EG∥FH∥CD, ∵AB∥FH,∴∠ABF=∠BFH, ∵FH∥CD,∴∠CDF=∠DFH, ∴∠BFD=∠DFH+∠BFH=∠CDF+∠ABF; 同理可得∠BED=∠DEG+∠BEG=∠ABE+∠CDE; ∵∠ABF=
∴∠BFD=∠DFH+∠BFH=∠CDF+∠ABF=
∴∠BED:∠BFD=3:2. 故选C. |
 过点E、F分别作AB的平行线EG、FH,由平行线的传递性可得AB∥EG∥FH∥CD, ∵AB∥FH,∴∠ABF=∠BFH, ∵FH∥CD,∴∠CDF=∠DFH, ∴∠BFD=∠DFH+∠BFH=∠CDF+∠ABF; 同理可得∠BED=∠DEG+∠BEG=∠ABE+∠CDE; ∵∠ABF=
∴∠BFD=∠DFH+∠BFH=∠CDF+∠ABF=
∴∠BED:∠BFD=3:2. 故选C. |
题目简介
如图,AB∥CD,∠ABF=23∠ABE,∠CDF=23∠CDE,则∠E:∠F=()A.2:1B.3:1C.3:2D.4:3-数学
题目详情