 (1)当
当
(2)当
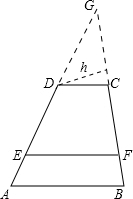
证明:延长AD、BC交于G,设△DCG在BC边上的高为h,则由三角形相似得:
(3)由于过点E平行于两底的水渠到两底的距离比等于2:3,由(2)中的结论可得: 水渠长=
由于过点F平行于两底的水渠到两底的距离比等于7:3,由(2)中的结论可得: 水渠长=
故两条水渠的总长度是180+240=420(米). |
 (1)当
当
(2)当
证明:延长AD、BC交于G,设△DCG在BC边上的高为h,则由三角形相似得:
(3)由于过点E平行于两底的水渠到两底的距离比等于2:3,由(2)中的结论可得: 水渠长=
由于过点F平行于两底的水渠到两底的距离比等于7:3,由(2)中的结论可得: 水渠长=
故两条水渠的总长度是180+240=420(米). |
题目简介
如图a,梯形ABCD中,AB∥CD,AB=a,CD=b,点E、F分别是两腰AD、BC上的点,且EF∥AB,设EF到CD、AB的距离分别为d1、d2,某同学在对这一图形进行研究时,发现如下事实:①当d1
题目详情
①当
当
当
当
②当
当
根据以上结论,解答下列问题:
(1)猜想当
(2)进一步猜想当
(3)如图b,有一块梯形耕地ABCD,AB∥CD,CD=100米,AB=300米,AD=500米,在AD上取两点E、F,使DE=200米,EF=150米,分别从E、F两处为起点开挖两条平行于两底的水渠,直到另一腰,求这两条水渠的总长度.