| (1)如图方案1,做∠B的角平分线BD交AC于点D,作∠BDC得角平分线DE交BC于点E, ∵∠A=36°, ∴∠C=∠ABC=72°, ∴∠DBC=36°,∠BDC=72°, ∴∠EDG=∠BDE=36°, ∴△ABD,△BDE,△DEC为等腰三角形; 如图方案2,做∠B的角平分线BF交AC于点F,作∠C得角平分线CM交BF于点M, ∵∠A=36°, ∴∠ACB=∠ABC=72°, ∴∠FBC=∠ABF=36°,∠FCM=∠MCB=72°, ∴∠CFM=∠CMF=72°, ∴△ABF,△BMC,△CMF为等腰三角形; 如图方案3,做∠C的角平分线CN交AB于点N,作∠BNC得角平分线NP交BC于点P, ∵∠A=36°, ∴∠ACB=∠ABC=72°, ∴∠BCN=∠ACN=36°,∠BNC=∠B=72°, ∴∠BNP=∠PNC=36°,∠NPB=72°, ∴△ANC,△NPC,△BNP为等腰三角形; 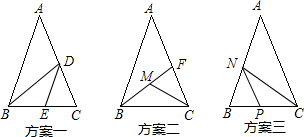 (2)①在图1中,作PN∥AB, ∵AB∥CD, ∴AB∥CD⊥PN, ∴∠1=∠BPN,∠3=∠NPD, ∴∠BPD=∠1+∠2, ∴∠1+∠3=∠2; ②在图2中,作PM∥AB,HQ∥CD, ∵AB∥CD, ∴AB∥CD∥PM∥HQ, ∴∠1=∠BPN,∠PQH=∠MPQ,∠HQC=∠4, ∴∠1+∠3=∠BPM+∠MPQ+∠4, ∴∠1+∠3=∠2+∠4; ③在图3中,作PE∥AB,OQ∥AB,MF∥CD, ∵AB∥CD, ∴AB∥CD∥PE∥OQ∥MF, ∴∠1=∠BPE,∠EPQ=∠PQO,∠OQM=∠QMF,∠FMD=∠5, ∴∠2=∠1+∠PQO,∠4=∠OQM+∠5, ∴∠1+∠3+∠5=∠2+∠4. 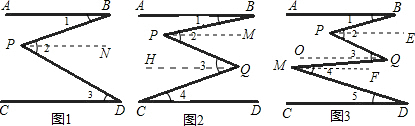 |
题目简介
(1)如图,在△ABC中,AB=AC,∠A=36°,请设计3种不同的方案,将△ABC分割成三个小等腰三角形.(2)如下图1、图2、图3,均有AB∥CD,则在图1中,∠1、∠2、∠3的关系是______
题目详情
(2)如下图1、图2、图3,均有AB∥CD,则
在图1中,∠1、∠2、∠3的关系是______;
在图2中,∠1、∠2、∠3、∠4的关系是______;
在图3中,∠1、∠2、∠3、∠4、∠5的关系是______;